平面直角坐标系
【课标要求】
|
考点 |
课标要求
|
知识与技能目标
|
|||
|
了解
|
理解
|
掌握
|
灵活应用
|
||
|
平面直角坐标系
|
理解平面直角坐标系的有关概念
|
|
∨
|
|
|
|
理解坐标平面内点的坐标特征并达到初步掌握
|
|
∨
|
∨
|
|
|
|
了解不同位置点的坐标特征并达到初步应用
|
∨
|
|
∨
|
∨
|
|
【知识梳理】
1.平面直角坐标系的有关概念:平面直角坐标系的有关概念不要死记硬背,应紧密结合坐标系来认识;在坐标平面内会正确地描点,对于坐标平面内的点要借助图形正确地写出,特别注意各象限内点的坐标符号。
2.坐标平面内点的坐标特征:注意两坐标轴上点的坐标的不同,且x轴、y轴不属于任何一个象限。
3.不同位置点的坐标特征:对于平行于两坐标轴的直线上点的坐标特点应借助于平面直角坐标系来应用。对于对称点的坐标特征应遵循:关于x轴对称的两点,横坐标不变,纵坐标相反; 关于y轴对称的两点,横坐标相反,纵坐标不变;关于原点对称的两点, 横纵坐标都互为相反数,或借助图形来完成,切忌死背。注意P(x,y)到两坐标轴的距离与线段长度的区分。
【能力训练】
一、填空题:
1.已知点M(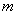 ,
,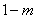 )在第二象限,则
)在第二象限,则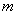 的值是 ;
的值是 ;
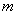 ,
,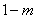 )在第二象限,则
)在第二象限,则 2.已知:点P的坐标是(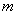 ,
, ),且点P关于
),且点P关于 轴对称的点的坐标是(
轴对称的点的坐标是(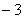 ,
,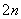 ),则
),则 ;
;
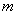 ,
, ),且点P关于
),且点P关于 轴对称的点的坐标是(
轴对称的点的坐标是(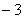 ,
,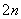 ),则
),则 ;
; 3.点 A在第二象限,它到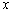 轴、
轴、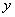 轴的距离分别是
轴的距离分别是 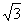 、
、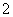 ,则坐标是 ;
,则坐标是 ;
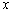 轴、
轴、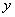 轴的距离分别是
轴的距离分别是 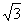 、
、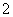 ,则坐标是 ;
,则坐标是 ; 4. 点P在 轴上对应的实数是
轴上对应的实数是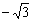 ,则点P的坐标是 ,若点Q在
,则点P的坐标是 ,若点Q在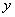 轴上对应的实数是
轴上对应的实数是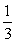 ,则点Q的坐标是 ,若点R(
,则点Q的坐标是 ,若点R(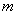 ,
,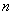 )在第二象限,则
)在第二象限,则 ,
, (填“>”或“<”号);
(填“>”或“<”号);
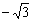 ,则点P的坐标是 ,若点Q在
,则点P的坐标是 ,若点Q在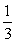 ,则点Q的坐标是 ,若点R(
,则点Q的坐标是 ,若点R(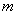 ,
,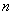 )在第二象限,则
)在第二象限,则 ,
, (填“>”或“<”号);
(填“>”或“<”号); 5.点P( ,
,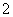 )关于
)关于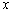 轴的对称点的坐标是 ,关于
轴的对称点的坐标是 ,关于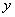 轴的对称点的坐标是 ,关于原点的对称点的坐标是 ;
轴的对称点的坐标是 ,关于原点的对称点的坐标是 ;
 ,
,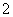 )关于
)关于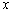 轴的对称点的坐标是 ,关于
轴的对称点的坐标是 ,关于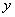 轴的对称点的坐标是 ,关于原点的对称点的坐标是 ;
轴的对称点的坐标是 ,关于原点的对称点的坐标是 ; 6.点A(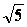 ,
,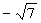 )到
)到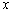 轴的距离是 ,到
轴的距离是 ,到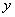 轴的距离是 ,到原点的距离是 ;
轴的距离是 ,到原点的距离是 ;
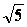 ,
,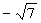 )到
)到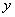 轴的距离是 ,到原点的距离是 ;
轴的距离是 ,到原点的距离是 ; 7.若点 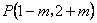 在第一象限,则
在第一象限,则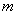 的取值范围是 ;
的取值范围是 ;
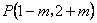 在第一象限,则
在第一象限,则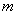 的取值范围是 ;
的取值范围是 ; 8.若 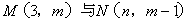 关于原点对称,则
关于原点对称,则 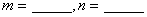 ;
;
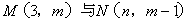 关于原点对称,则
关于原点对称,则 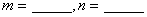 ;
; 9.已知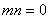 ,则点(
,则点(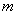 ,
,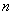 )在 ;
)在 ;
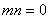 ,则点(
,则点(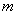 ,
,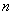 )在 ;
)在 ; 10.等腰三角形周长为20cm,腰长为 (cm),底边长为
(cm),底边长为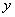 (cm),则
(cm),则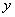 与
与 的函数关系式为 ,自变量
的函数关系式为 ,自变量 的取值范围是 ;
的取值范围是 ;
 (cm),底边长为
(cm),底边长为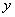 (cm),则
(cm),则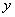 与
与 的函数关系式为 ,自变量
的函数关系式为 ,自变量 的取值范围是 ;
的取值范围是 ; 11.已知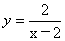 中自变量
中自变量 的取值范围是 ;
的取值范围是 ;
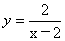 中自变量
中自变量 的取值范围是 ;
的取值范围是 ; 12.函数 中自变量
中自变量 的取值范围是__ ___;
的取值范围是__ ___;
 中自变量
中自变量 的取值范围是__ ___;
的取值范围是__ ___; 13.函数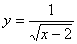 中,自变量
中,自变量 的取值范围是 ;
的取值范围是 ;
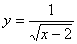 中,自变量
中,自变量 的取值范围是 ;
的取值范围是 ; 14.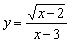 中自变量
中自变量 的取值范围是 ;
的取值范围是 ;
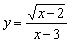 中自变量
中自变量 的取值范围是 ;
的取值范围是 ; 15.函数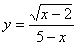 中自变量
中自变量 的取值范围是_____ ___;
的取值范围是_____ ___;
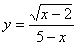 中自变量
中自变量 的取值范围是_____ ___;
的取值范围是_____ ___; 16.函数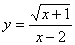 中自变量
中自变量 的取值范围是 ;
的取值范围是 ;
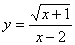 中自变量
中自变量 的取值范围是 ;
的取值范围是 ; 18.函数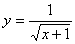 中,自变量
中,自变量 的取值范围是________ __;
的取值范围是________ __;
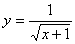 中,自变量
中,自变量 的取值范围是________ __;
的取值范围是________ __; 19.函数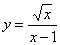 的自变量
的自变量 的取值范围是 ;
的取值范围是 ;
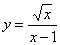 的自变量
的自变量 的取值范围是 ;
的取值范围是 ; 20.函数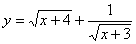 的自变量
的自变量 的取值范围是 ;
的取值范围是 ;
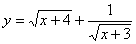 的自变量
的自变量 的取值范围是 ;
的取值范围是 ;| 中考政策 | 中考状元 | 中考饮食 | 中考备考辅导 | 中考复习资料 |

